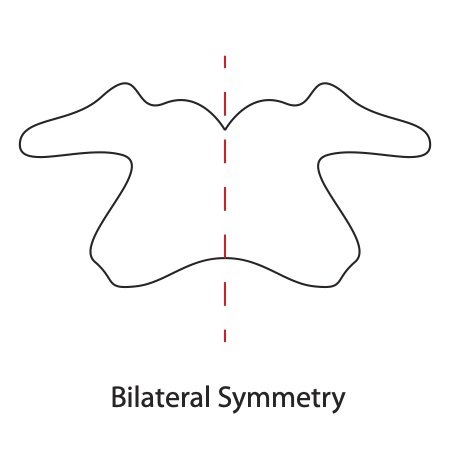
Butterfly Problem

A complex solution to the Lamp Project is called the Butterfly Problem, discovered when a student wanted their intersecting extensions to make bilaterally symmetrical butterflies. This is not the norm for the project because it means that the designer cannot simply make a module from identical repeating extensions. Instead, extensions in mating pairs must be mirrored to the other. One extension in a pair would need to be left-handed, and the other right handed (bilateral symmetry). Whereas normally, identical extensions cross one another forming rotational symmetry.

The Butterfly Problem is esoteric, and worth investigating if you like a challenge and are interested in geometrical problem solving. The challenge is not in simply making sure each edge pair is going to be bilaterally symmetrical, it is in designing the simplest and most elegant solution to the problem.

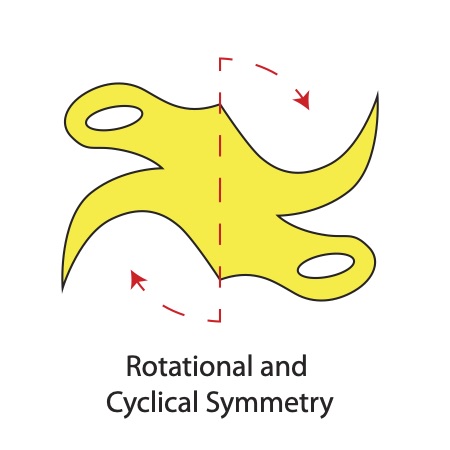
Mirror Versus Rotational and Cyclical Symmetry

As seen below, The edges of mated polygons in the lamp project make up the axis of symmetrical relationships. With the butterfly problem, bilateral symmetry is necessary where there is a mirror of the shape reflected about two polygon's mated edges. The standard lamp module is made from replicated units that are not reflected; instead, they are rotated.

Diffficult Polyhedra

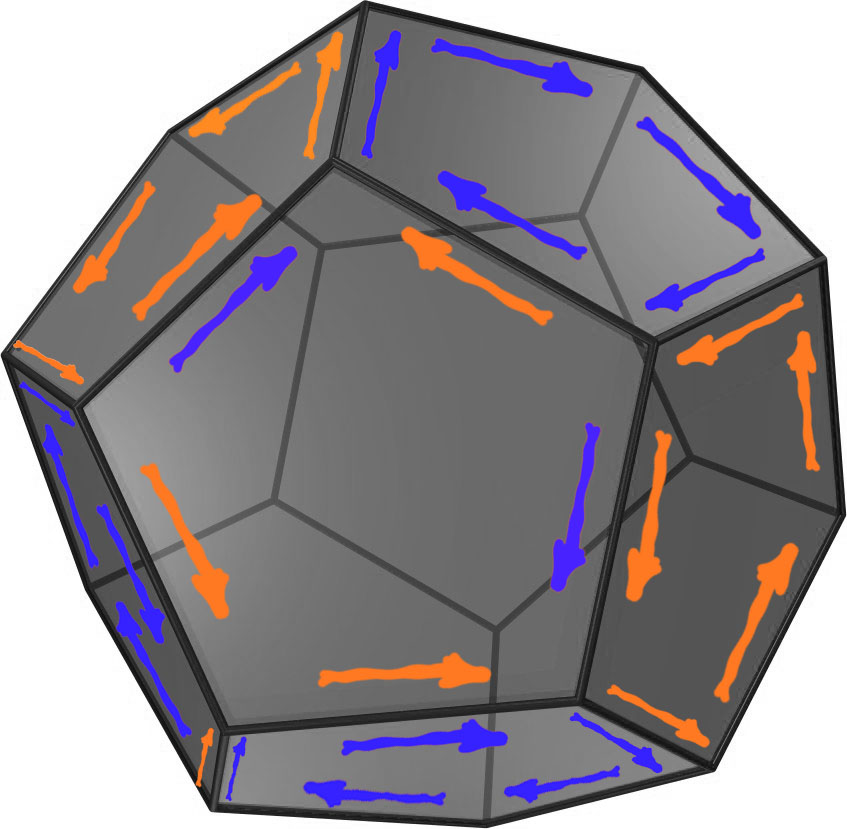
If the base polyhedron is made only from repeating polygons with odd numbers of edges, such as pentagons, then a serious challenge arises when trying to lay out repeating modules. As seen in the image below, a dodecahedron cannot repeat the modules. Two of its polygons have five orange arrows; two have five purple arrows. The front face has three orange arrows and two purple arrows, and the lower left polygon has one orange and four purple arrows. The six remaining polygons on the opposite side have yet to be planned out, but it can be noted that any mating edges of those polygons must have arrows of opposite colors to the ones they mate with.

Further, the odd number of edges (5) on the pentagon makes it impossible to place arrows in a pattern that alternates all the way around. If you make Edge1 orange; then Edge2 would be purple; Edge3 would be orange; Edge4 would be purple, and Edge5 would be orange... but Edge5 abuts Edge1, and both would be orange. It is not possible to use this same reversing arrow pattern on all of the other faces in hopes of aligning bilaterally mating pairs, as there will come an instance where mating arrows will not be opposite colors.

Interestingly, a cube does not have the same problem as the dodecahedron or the other Platonic solids because it is made from squares, which have an even number of edges.

Easy Polyhedra

The Butterfly Problem can be easily overcome when utilizing polyhedra made from at least two unique types of polygons... as long as the edges of like polygons only mate with the edges of unlike polygons. The icosadodecahedron, below, demonstrates that no triangle edge connects to another triangle edge, and no pentagon edge connects to another pentagon edge. Therefore, all triangles can be right handed and all pentagons can be left handed.

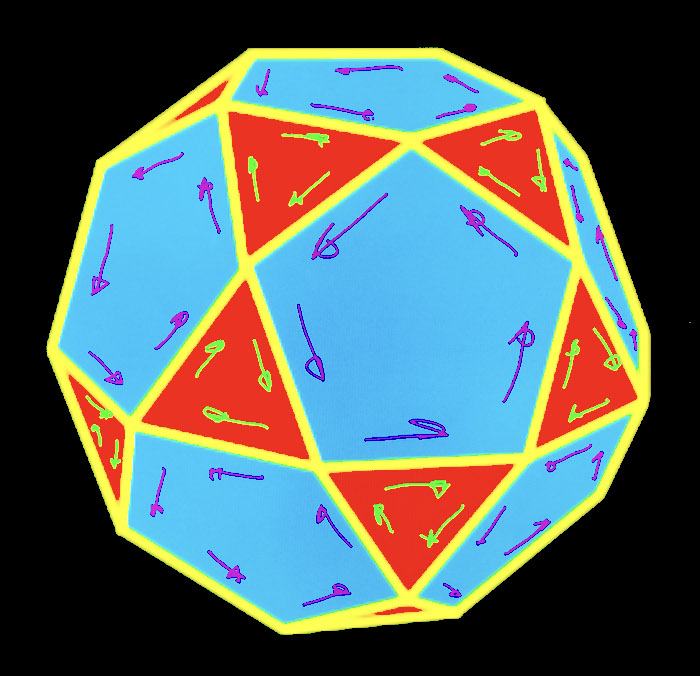
The subject of Butterfly Mirroring in the Lamp project is in its infancy, and many more unique problems and solutions may be discovered. It is an interesting problem to figure out how this bilateral symmetry problem can be addressed when working with other base polyhedra, such as the truncated icosahedron and truncated dodecahedron - both have two unique styles of polygons in their design, but only one type is completely surrounded by the other. What happens with their edge pairings? And how about volumes made from three or more unique polygons?