Duals

A 10-second video showing the cube-octahedron Dual Relationship. This video was created by Takashiyoshinorw (youtube.com.@takashiyoshinorw).

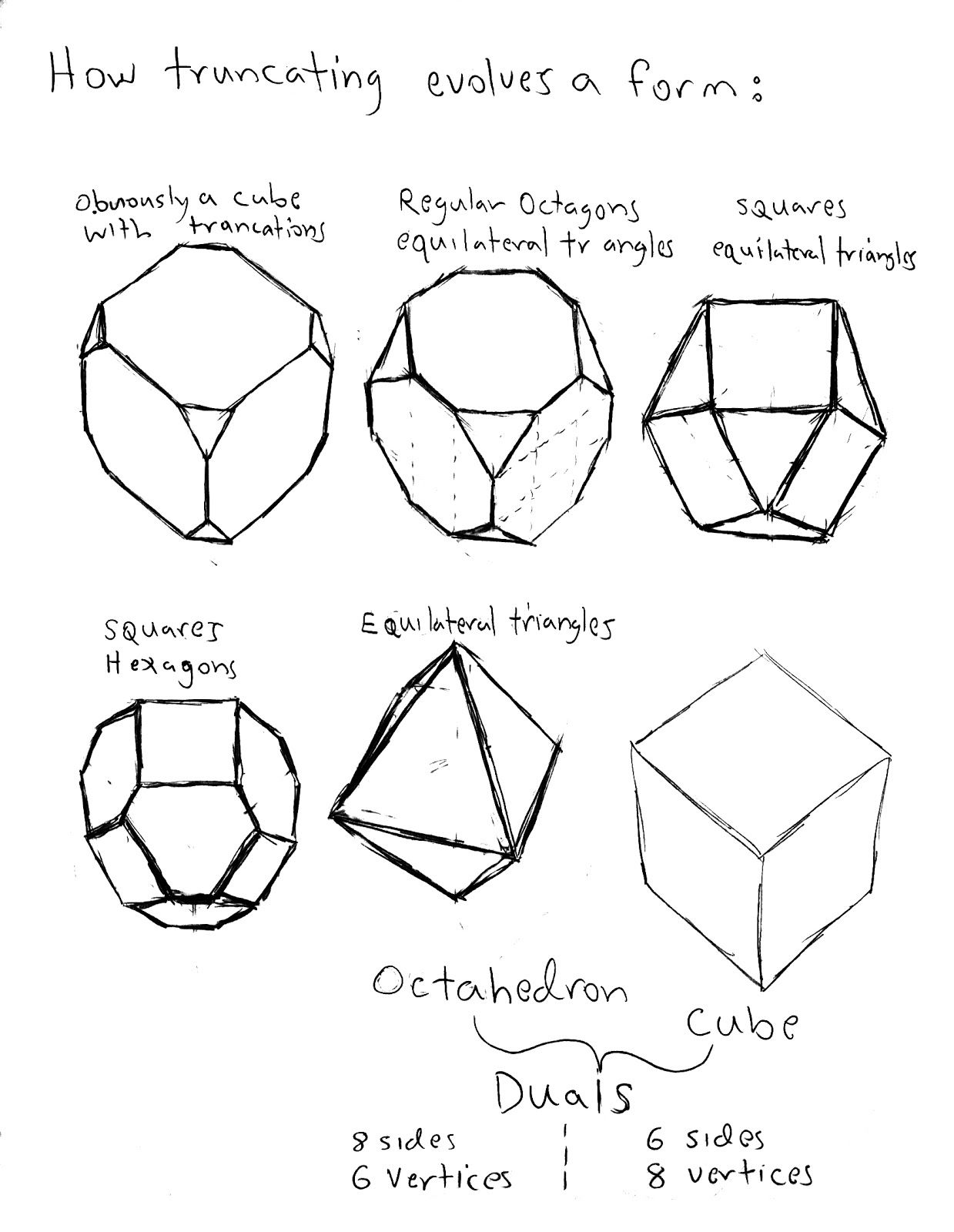
Duals in 3D geometry are two forms that have a special relationship between each other. In the case of the Platonic Duals, it is the relationship of faces to verticies. An interesting aspect of the dual relationship is that in both of the dual shapes, the number of edges are the same. What this means in the TGF Project is that a cube can turn into an octahedron, and visa versa, by truncation or stellation. As seen in the short video, above, vertiices turn into faces, and faces turn into verticies.

There are innumerable half-way transitions between duals; some of which are distinctly well proportioned, such as the Cuboctahedron.

Here is a list of the Platonic Duals:

Tetrahedron - Tetrahedron

The Tetrahedron has 4 faces and 4 verticies. It also has 6 edges.

Cube - Octahedron

The Cube has 6 faces and 8 vertices. The Octahedron has 8 faces and 6 verticies. They both have 12 edges.

* Dodccahedron - Icosahedron

The Dodecahedron has 12 faces and 20 vertices. The Iconshedron has 20 faces and 12 verticies. They both have 30 edges.