CUBE: Drawing to Assembly

25 minute video on drawing, cutting, folding and gluing a cube pattern..

The above video describes in detail every step in creating a cube from paper. It uses the "cross" style pattern for the cube, but the methods are valid for any cube pattern you choose. With some of the other patterns, you may wish to make sure some of your lines are accurately perpendicular, though with careful compass work that should automatically happen.

Notice that at no point was a ruler used (instead I used a straight edge), nor was any numerical measurement made.

The tools used in the video are:

1. cutting surface
2. straight edge
3. pencil
4. eraser
5. compass
6. craft knife
7. glue

How a Cube Pattern is Derived

Reverse-Engineering

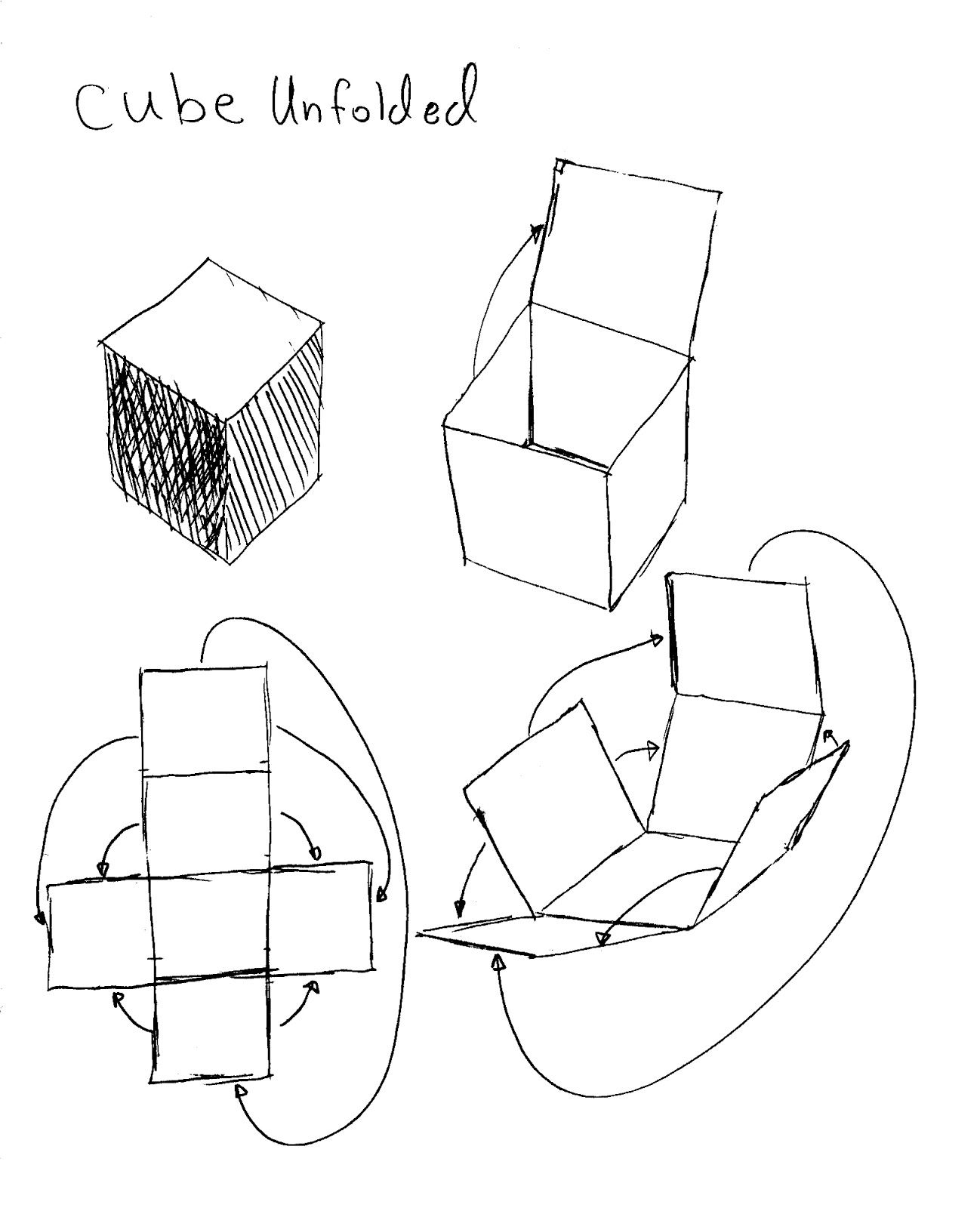
Making a cube or any other geometric volume from folded paper takes an understanding of the relationships between individual planes. As seen above, the various sides of the cube attach at its edges in specific ways, meaning that each side has connective relationships. In fact, each face of a cube has four other faces that it ultimately attaches to along its edges, which implies that it can be placed in four alternate locations within a pattern. Notice how the "lid" is opened, then the 'sides" are folded away, and the cross pattern is revealed? This visualization exercise can be done by looking at a closed geometric form, then using your imagination to animate how it may unfold.

Reverse-engineering is when you start with a final object and take it apart to figure out how it was made.

Evolving The Layout

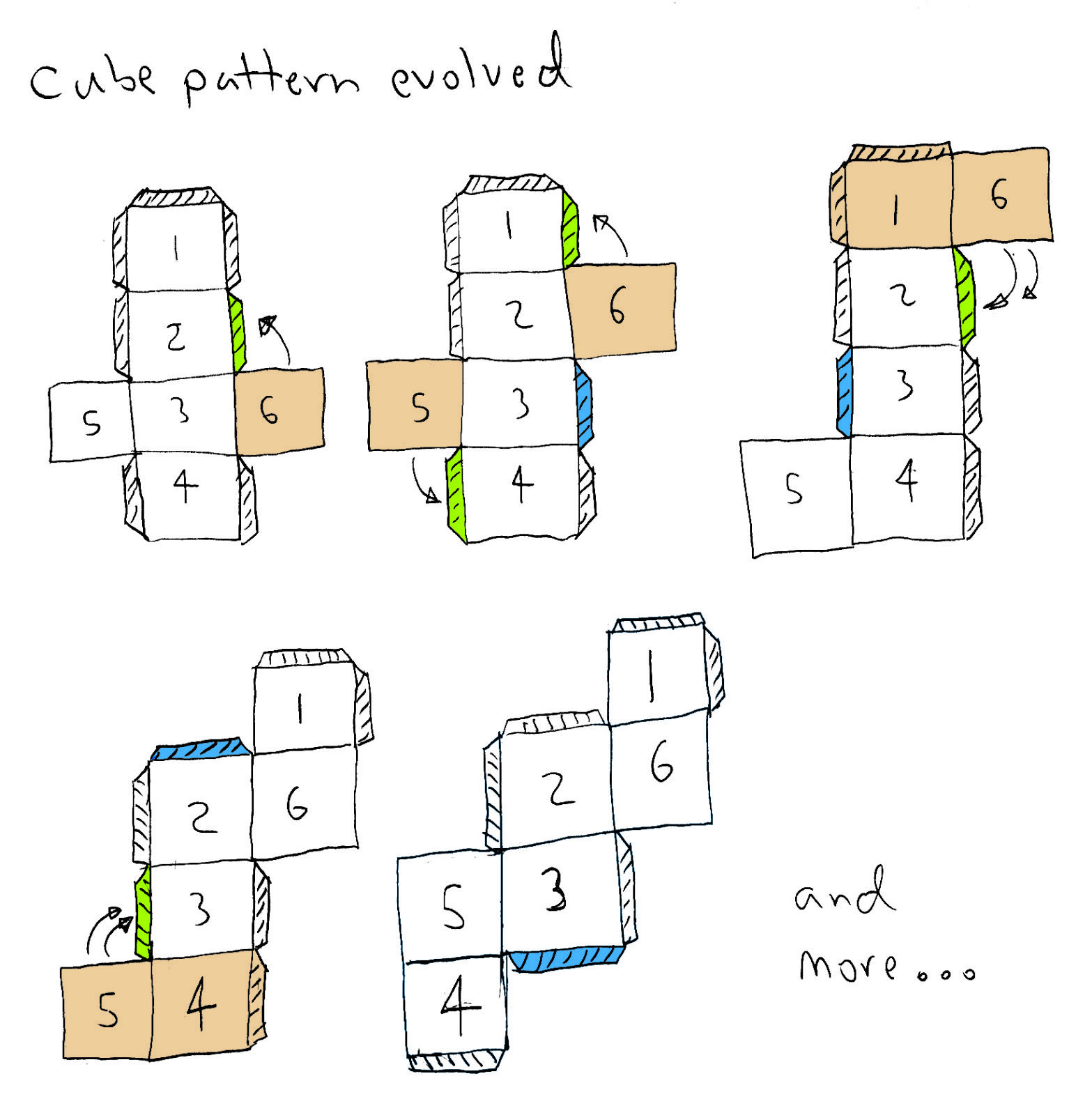
In the image, above, the pattern's layout evolves through a series of iterations. The squares are shifted to new locations, where they ultimately would be attached anyway when the cube is assembled. These patterns each contain tabs, or the small extra surfaces that allow the paper patttern to be glued-up. If the pattern was made of wax instead of paper, the tabs may not be necessary, as the edges could be melted together. If the pattern was sheet steel, it could be welded, etc. But with paper, tabs are very important.

Notice that the green colored tabs are locations where the light brown sides will be moved, thus eliminating that tab. However, when a tab is eliminated another must created where the side used to be connected, as shown in blue.

Your cube pattern can be made in any way you see fit, as long as the pattern is able to be folded into its ultimate form without superfluous tabs or erroneous sides. The lessons shown here apply to any TGF form that you create.

Designing Tabs

Tabs need to be located wherever two edges will ultimately connect. However, only one tab per connection is required. In fact, one is better than two, as it is easier to assemble and makes a neater result. Consider which pairing edge should have the tab. There are several factors that will determine their placement:

1. As noted, above, there is one tab per edge connection, thus there is always an equal number of tabbed and untabbed edges in a pattern. This also means that there will always be an even number of disconnected edges in a pattern (since two always pair up). Knowing this can help you reslove yout tab layout. Note though that there may be either an odd or even number of tabs!
2. Is there room on your pattern to place a tab in a desired location? If not, it will need to be moved to its alternate location.
3. Design your pattern so that tabs are easiest to use. In the process of assembly, will the tab location make it easier to put together? For example, when the last face of the cube is being glued in place, are the remaining tabs going to be easy or difficult to access?
4. If you forget a tab, add one with a strip of paper, rather than redrawing the enitre pattern from scratch.
5. If you found that you created too many tabs, cut the extras off rather than trying to glue two together, as it will make a better result and be easier to do.
6. Tab shape, width and depth make a difference.
   1. It should go the full width of the edge it is attached to, but be tapered at its ends for ease of fitting.
   2. A tab that is too shallow is fragile, warps easily when wetted with glue, and is difficult to hold in place during glue setting.
   3. A tab that is too deep is awkward to fit, requires more paper, and sometimes is confused with being a side.
   4. Tab depth relates proportionally to the size of your object. The smaller the object the smaller the tab, ect. Typical tab depth in the classroom ranges from 1/4" to 3/8", or about a centimeter.
7. There is no need to actually measure the depth of a tab, as it works fine to draw them out by eye.
8. Tabs can be drawn freehand, or with a ruler. Both methods work well if you can draw relatively accurate lines freehand.